Chapter 10 Algebraic Expressions Solutions

NCERT Solutions: Algebraic Expressions

Exercise 10.1

Q.1. Get the algebraic expressions in the following cases using variables, constants, and arithmetic operations: 
(i) Subtraction of z from y. 

Ans: y – z

(ii) One-half of the sum of numbers x and y.

Ans: (x + y)/2

(iii) The number z multiplied by itself. 

Ans: Z²

(iv) One-fourth of the product of numbers p and q. 

Ans: pq/4

(v) Numbers x and y both squared and added. 

Ans: x² + y²

(vi) Number 5 added to three times the product of m and n. 

Ans: 5 + 3(mn) = 5 + 3mn 

(vii) A product of numbers y and z subtracted from 10. 

Ans: 10 – yz

(viii) Sum of numbers a and b subtracted from their product. 

Ans: ab – (a + b)

Q.2. (i) Identify the terms and their factors in the following expressions, show the terms and factors by tree diagram: 
(a) x – 3

Ans: Terms: x, -3

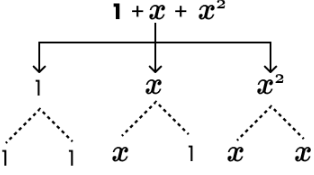
(b) 1 + x + x²
Ans: Terms: 1, x, x²

(c) y – y³

Ans: Terms: y, -y³

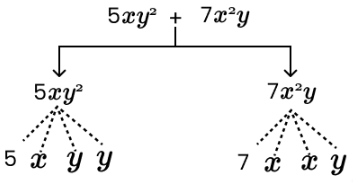
(d) 5xy² + 7x²y

Ans: Terms: 5xy² , 7x²y

(e) -ab + 2b² – 3a²

Ans: Terms:  -ab, 2b², -3a²

(ii) Identify the terms and factors in the expressions given below: 

(a) -4x + 5

Ans: In the expression -4x + 5, there are two terms: -4x and 5. 
The factors of the first term -4x are -4 and x, while the second term 5 is a constant.

(b) -4x + 5y 

Ans: In the expression -4x + 5y, we can identify the following: 
Terms: The terms are -4x and 5y. 
Factors: For the term -4x, the factors are -4 and x. For the term 5y, the factors are 5 and y.

(c) 5y + 3y²

Ans: 
The expression 5y + 3y² consists of two terms: 5y and 3y². The factors of these terms are as follows: For the term 5y, the factors are 5 and y. For the term 3y², the factors are 3, y. Thus, the complete breakdown of the factors is: 5y: 5, y 3y²: 3, y.

(d) xy + 2x²y²

Ans: 

The expression xy + 2x²y² consists of two terms: xy and 2x²y². The factors of these terms are as follows: For the term xy, the factors are x and y. For the term 2x²y², the factors are 2, x and y.

(e) pq + q

Ans:  In the expression pq + q, there are two terms: pq and q. The factors of these terms are as follows: The term pq consists of the factors p and q. The term q is a single factor.

(f) 1.2ab – 2.4b + 3.6a

Ans: 

Terms: The expression consists of three terms: 1.2ab, -2.4b, and 3.6a. Factors: The factors of each term are as follows: for 1.2ab, the factors are 1.2, a, and b; for -2.4b, the factors are -2.4 and b; and for 3.6a, the factors are 3.6 and a. 

(g)  

(h) 0.1 p² + 0.2q² 

Q.3. Identify the numerical coefficients of terms (other than constants) in the following expressions: 
(i) 5 – 3t²
(ii) 1 + t + t² + t²
(iii) x + 2xy + 3y
(iv) 100m + 1000n
(v) -p²q² + 7pq
(vi) 1.2a + 0.8b
(vii) 3.14 r²
(viii) 2(l + b)
(ix) 0.1y + 0.01y²

^Ans: 

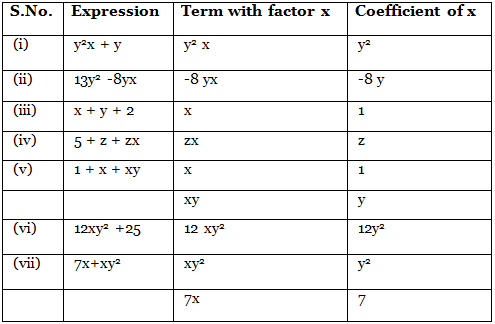
Q.4. (a) Identify terms which contain x and give the coefficient of x. 
(i) y²x + y
(ii) 13y² – 8yx
(iii) x + y + 2
(iv) 5 + z + zx
(v) 1 + x + xy
(vi) 12xy² + x25
(vii) 7x + xy²

Ans: 

(b) Identify terms which contain y² and give the coefficient of y^2.
(i) 8 – xy²
(ii) 5y² + 7x
(iii) 2x²y – 15xy² + 7y²

Ans:

Q.5. Classify into monomials, binomials and trinomials: 
(i) 4y – 7x
(ii) y²
(iii) x + y – xy
(iv) 100
(v) ab – a – b
(vi) 5 – 3t
(vii) 4p²q – 4pq²
(viii) 7mn
(ix) z² – 3z + 8
(x) a² + b²
(xi) z² + z
(xii) 1 + x + x²

^Ans: 

 
Q.6. State whether a given pair of terms is of like or unlike terms: 

(i) 1,100
(ii) 
(iii) -29x, -29y
(iv) 14xy, 42 yx
(v) 4m²p, 4mp²
(vi) 12xz, 12x² z²

^Ans: 

Q.7. Identify like terms in the following: 
(a) -xy², -4yx², 8x², 2xy², 7y,  -11x²  – 100x, – 11yx, 20x²y, -6x², y, 2xy, 3x

Ans: Like terms are:
(i) -xy²,2 xy²
(ii) –4yx² , 20x²y
(iii) 8x²,-11x²,-6x²
(iv) 7y, y
(v) -100x, 3x
(vi) -11yx, 2xy

(b) 10pq, 7p, 8q, -p²q², -7qp, -100q, -23, 12q²p², -5p², 41,2405 p, 78qp, 13p²q, qp², 701p²

^{Ans: Like terms are:}

(i) 10 pq – 7 pq, 78 pq
(ii) 7p, 2405 p
(iii) 8q, -100q
(iv) -p²q², 12p²q²
(v) -12,41
(vi) -5p²,701p²
(vii) 13 p²q, qp²

Exercise 10.2

Q1: If m = 2, find the value of: 
(i) m – 2    
(ii) 3m – 5    
(iii) 9 – 5m
(iv) 3m² – 2m – 7
(v) 
Ans: 
(i) m – 2 = 2 – 2    [Putting m = 2]
= 0

(ii) 3m – 5 = 3 x 2 – 5     [Putting m = 2]
= 6 – 5 = 1

(iii) 9 – 5m = 9 – 5 x 2    [Putting m = 2]
= 9 – 10 = – 1

(iv) 3m² – 2m – 7
= 3(2)² – 2 (2) – 7 [Putting m = 2]
= 3 x 4 – 2 x 2 – 7
 = 12-4-7
 = 12- 11 = 1

(v)    [Putting m = 2]
= 5 – 4 = 1

Q2: If p = -2, find the value of:
(i) 4p + 7
(ii) – 3p² + 4p + 7
(iii) -2p³ – 3p² +4/7 + 7
Ans: 
(i) 4p + 7 = 4 (- 2) + 7    [Putting p= -2]
= -8 + 7 = -1

(ii) -3p² + 4p + 7
= -3 (-2)²+ 4 (-2) + 7 [Putting p = – 2]
= – 3 x 4 – 8 + 7
= – 12 – 8 + 7
= -20 + 7 = -13

(iii) – 2p³ – 3p² +4p + 7
= – 2 (-2)³ – 3(-2)² + 4 (-2) + 7 [Putting p = – 2]
= -2  x (-8) – 3 x 4 – 8 + 7
= 16 – 12 – 8 + 7
= -20  + 23 = 3

Q3: Find the value of the following expressions, when x = -1: 
(i) 2x – 7
(ii) -x + 2
(iii) x² + 2x + 1
(iv) 2x²– x – 2
Ans: 
(i) 2x – 7 = 2 (-1) – 7      [Putting x= – 1]
= – 2 – 7 = – 9

(ii) – x + 2 = – (-1) + 2     [Putting x= – 1]
= 1 + 2 = 3

(iii) x² + 2 x + 1 = (-1)² + 2 (-1) + 1 [Putting x= – 1]
= 1 – 2 + 1
= 2 – 2 = 0

(iv) 2x²– x – 2 = 2 (-1)² – (-1) – 2 [Putting x= – 1]
= 2×1 + 1-2
= 2 + 1 – 2
= 3 – 2 = 1

Q4: If a = 2,b = -2, find the value of: 
(i) a² + b² 
(ii) a²+ab + b²
(iii) a² – b²
Ans: 
(i) a² + b² ( 2)² + (- 2)² [Putting a = 2. b = – 2 ]
= 4 + 4 = 8

(ii) a²+ab + b² 
= (2) + ( 2) (- 2) +(-2)²   [Putting a = 2. b = – 2 ]
= 4 – 4 + 4 = 4

(iii) a² – b² = (2)² – (-2)² [Putting a = 2,b = – 2]
= 4 – 4 = 0

Q5: When a = 0, b = -1, find the value of the given expressions: 
(i) 2a + 2b
(ii) 2a²+b²+1
(iii) 2a²b + 2ab² +ab
(iv) a²+ab+2
Ans: 
(i) 2a + 2b = 2 (0) + 2 (-1)    [Putting a – 0,b = – 1]
= 0 – 2 = -2  

(ii) 2a² + b² + 1 = 2 (0)² + (-1)² + 1 [Putting a – 0,b = – 1]
= 2 x 0 + 1+ 1 = 0 + 2 = 2

(iii) 2a²b + 2ab² + ab = 2(0)² (-1) + 2 (0 )(-1)² + (0 )(-1) [Putting a = 0,b = – 1]
= 0 + 0 + 0 = 0

(iv) a² +ab + 2 – (0)² + (0) (-1) + 2 [Putting a – 0,b = – 1]
= 0 + 0 + 2 = 2

Q6: Simplify the expressions and find the value if x is equal to 2: 
(i) x + 7 + 4 (x- 5)
(ii) 3 (x + 2) + 5x – 7
(iii) 6x + 5 (x – 2)
(iv) 4 (2x – 1) + 3x + 11
Ans: 
(i) x + 7 + 4(x- 5) = x + 7 + 4x – 20 = x + 4 x + 7 – 20
= 5 x – 13 = 5 x 2 – 13                            [Putting x = 2]
= 10-13 = -3

(ii) 3 (x+ 2) + 5x – 7 = 3x + 6 + 5x -7 = 3x + 5x + 6 – 7
= 8x – 1 = 8 x 2 – 1                    [Putting x = 2]
= 16 – 1 = 15

(iii) 6x + 5 (x – 2) = 6x + 5x -10 = 11x – 10
= 11 x 2 – 10                      [Putting x = 2]
= 22 – 10 = 12

(iv) 4(2x – 1) + 3x + 11 = 8x – 4 + 3x +11 = 8x + 3a – 4 + 11
= 11a + 7 = 11 x 2 + 7 [Putting x = 2]
= 22 + 7 = 29

Q7: Simplify these expressions and find their values if x = 3,a = -1, b = – 2 :
(i) 3x – 5 – x + 9
(ii) 2 – 8x + 4x + 4
(iii) 3a + 5 – 8a + 1
(iv) 10 – 3b – 4 – 5b
(v) 2a – 2b – 4 – 5 + a
Ans: 
(i) 3x – 5 – x + 9 = 3x – x – 5 + 9 = 2x + 4
= 2 x 3 + 4         [Putting x = 3]
= 6 + 4 = 10

(ii) 2 – 8x + 4x + 4 = – 8x + 4x + 2 + 4 = -4x + 6
= – 4 x 3 + 6     [Putting x = 3]
= -12 + 6 = -6

(iii) 3a + 5 – 8a + 1 = 3a – 8a + 5 + 1 = – 5a + 6
= -5(- 1) + 6       [Putting a = – 1]
= 5 + 6 = 11

(iv) 10 – 3b – 4 – 5b = – 3b – 5b + 10 – 4 = -8b+6
= -8 (-2)+ 6    [Putting b = -2]
= 16 + 6 = 22

(v) 2a – 2b – 4 – 5 + a = 2a + a – 2b – 4 – 5
= 3a – 2b – 9 = 3 (-1)-2 (-2) -9    [Putting a = -1 , b = – 2]
= -3 + 4 -9 = -8

Q8: 
(i) If z = 10, find the value of z³ – 3 (z – 10).
(ii) If p = – 10, find the value of p² – 2p – 100
Ans:
(i) z³ -3(z-10) = (10)³-3(10 – 10) [Putting z = 10]
= 1000 – 3 x 0 = 1000- 0
= 1000

(ii) p² – 2p – 100 = (-10)² – 2 (-10) – 100    (Putting p = – 10]

= 100+ 20 – 100 = 20

Q9: What should be the value of a if the value of 2x² + x – a equals to 5, when x = 0 ? 
Ans: 
Given: 2x² + x – a = 5
⇒ 2 (0)² + 0 – a = 5 [Putting x = 0]
⇒ 0 + 0 – a = 5
⇒ a = -5
Hence, the value of a is -5.

Q10: Simplify the expression and find its value when a = 5 and b = – 3: 2 (a² + ab) + 3 – ab
Ans:
Given: 2 (a² + ab) + 3 – ab
⇒ 2a² + 2ab + 3 – ab
⇒ 2a² + 2ab – ab + 3
⇒ 2a² + ab + 3
⇒ 2 (5)² + (5) (-3) + 3 [Putting a = 5 , b = -3]
⇒ 2 x 25 – 15 + 3
⇒ 50 – 15 + 3
⇒ 38