Chapter Notes: Large Numbers Around Us

Have you ever thought about how many grains of rice are in a single bag, or how many stars twinkle in the night sky? Numbers are everywhere, helping us count, measure, and understand the world around us. Sometimes, these numbers are small, like the number of fingers on your hand. But often, especially when we talk about populations, distances between cities, or even the variety of life on Earth, the numbers become very, very large!

Imagine a farmer named Eshwarappa, walking through a market in Karnataka. He overhears a conversation about rice – not just any rice, but lakhs of varieties that used to exist in India! A lakh!Eshwarappa hearing a conversationThat sounds like a huge number. Eshwarappa Eshwarappa shared this incident with his daughter Roxie and son Estu . They wonder, 

“Can a person taste all 1 lakh rice varieties in their lifetime?”

Let’s Calculate!

There are 365 days in a year.
So if someone lives for 100 years, the number of days is:100×365=36,500 days.

So, if someone eats 3 different types of rice every single day for 100 years, they can taste all 1 lakh rice varieties!
This story from your textbook introduces us to the fascinating world of large numbers. It makes us question: How big is a lakh? How do we even write or say such big numbers?

In this chapter, we will embark on a journey to explore these “Large Numbers Around Us.” 

Getting a Feel for Large Numbers

Sometimes, we hear big numbers like 180 metres or 450 metres—but it’s hard to imagine how tall that really is. So we compare it to something we know.

Let’s Look at Somu’s Building

• Somu is 1 metre tall.
• Each floor is about 4 times his height.
  So, 1 floor = 4 metres.

There are 10 floors, so the total height of the building is:

10×4=40 metres

Q1: Which is taller — The Statue of Unity or Somu’s building? How much taller?

• Statue of Unity = 180 metres
• Somu’s building = 40 metres

180−40=140180−40=140 metres taller

Answer: The Statue of Unity is taller by 140 metres.

Q2: How much taller is the Kunchikal waterfall than Somu’s building?

• Waterfall height = 450 metres
• Building height = 40 metres

450−40=410450−40=410 metres taller

Answer: The waterfall is 410 metres taller than Somu’s building.

Q3: How many floors should Somu’s building have to be as tall as the waterfall?

• Waterfall = 450 metres
• 1 floor = 4 metres

450÷4=112.5450÷4=112.5

We can’t have half a floor in reality, so we round up to 113.

Answer: Somu’s building should have 113 floors to be as tall as the waterfall!

Is One Lakh a Very Large Number?

This is actually a very interesting question because…

Sometimes 1 lakh feels very big and sometimes it feels small, depending on what we are talking about.

Let’s see why:

Roxie gives three examples to show how huge one lakh can feel:

1. 1 Lakh Varieties of Rice
   • Imagine tasting a new type of rice every day.
   • It would take 274 years to try them all!
   • We live only about 70–80 years. So, we’ll never finish them!
2. Living for 1 Lakh Days
   • One year has 365 days.
   • 1,00,000 ÷ 365 ≈ 274 years!
   • That’s like living three lifetimes. So yes, it’s big.
3. 1 Lakh People Standing in a Line
   • If each person takes about 0.38 meters of space, then:
   • 1,00,000 people = 38 km long line.
   • That’s like a line from one city to another!

Estu gives a different view. He shows how small 1 lakh can feel:

1. Stadium Seats
   • The cricket stadium in Ahmedabad holds more than 1 lakh people.
   • They all fit in one place — that feels not so big, right?
2. Hair on a Human Head
   • An average person has 80,000 to 1,20,000 hairs.
   • That means 1 lakh hairs fit on your head!
   • So, in a tiny space, you can already have 1 lakh things.
3. Fish Eggs
   • Some fish can lay 1 lakh eggs at once!
   • Even 10 lakh (a million) in some species!
   • That makes 1 lakh seem small in nature.

Q: So, is 1 lakh big or small?

Ans: It depends on what you’re comparing it with.

• If you’re saving ₹1 lakh, it feels like a lot of money.
• But if a government spends ₹1 lakh on a city, it’s very little.
• If you’re counting people or things in small spaces, 1 lakh may not feel big.
• But if you want to do something 1 lakh times, it’s a huge effort.

Reading and Writing Large Numbers 

Now that we have a better feel for large numbers like lakhs, how do we actually read and write them clearly? 

The Indian Place Value System

In the Indian system, numbers are grouped into hundreds, thousands, lakhs, crores, and so on. Here’s a breakdown:

• Units: The first three digits from the right are the units, tens, and hundreds.
• Thousands: The next two digits are the thousands.
• Lakhs: The next two digits are the lakhs.
• Crores: The digits after lakhs are the crores.

Indian Place Value Chart

Comma Rules:

1. The first comma comes after 3 digits from the right (thousands group).
2. Next commas come after 2 digits each.

Example:
12,78,830 is grouped as 12 (lakhs), 78 (thousands), 830 (hundreds & below)

Q: Write these in words:

(a) 3,00,600
Ans: Three lakh six hundred

(b) 5,04,085
Ans: Five lakh four thousand eighty-five

(c) 27,30,000
Ans: Twenty-seven lakh thirty thousand

(d) 70,53,138
Ans: Seventy lakh fifty-three thousand one hundred thirty-eight

Writing Number Names as Numbers

Now let’s go the other way — you are given the number in words, and you need to write it in figures (numbers).

Q: Write the numbers

(a) One lakh twenty-three thousand four hundred and fifty-six
Ans: 1,23,456

(b) Four lakh seven thousand seven hundred and four
Ans: 4,07,704

(c) Fifty lakhs five thousand and fifty
Ans: 50,05,050

(d) Ten lakhs two hundred and thirty-five
Ans: 10,00,235

Try yourself:

What is the height of Somu’s building?

• A.40 metres
• B.180 metres
• C.450 metres
• D.100 metres

View Solution

 The Land of Tens

Understanding place value is like having a secret code for numbers. Each digit in a number holds a specific value based on its position. The “Land of Tens” analogy from the chapter helps illustrate this beautifully using special calculators.

Imagine calculators with limited buttons:

• Thoughtful Thousands (+1000 button): To make 3,000, you press it 3 times. To make 10,000, you press it 10 times. To make one lakh (1,00,000), you need to press it 100 times (since 1 lakh = 100 thousands).

• Tedious Tens (+10 button): To make 500, you press it 50 times (50 x 10 = 500). To make 1,000, you press it 100 times (100 x 10 = 1000). To make one lakh (1,00,000), you need a whopping 10,000 presses (10,000 x 10 = 1,00,000)!
• Handy Hundreds (+100 button): To make 3,700, you press it 37 times (37 x 100 = 3700). To make 10,000, you press it 100 times (100 x 100 = 10,000). To make one lakh (1,00,000), you press it 1,000 times (1,000 x 100 = 1,00,000).

This shows how many smaller units make up larger ones: 100 thousands make a lakh, 10,000 tens make a lakh, and 1,000 hundreds make a lakh.

What is Place Value? 

Place value defines the value of each digit in a number based on its position. Each position, or “place,” in a number has a unique value that helps determine the overall number.

Example 1: What are the place values of each digit in the number 92,735?
Ans: 

• 5 is Ones
• 3 is Tens
• 7 is Hundreds
• 2 is Thousands
• 9 is Ten thousands

The diagram below illustrates the above example in more detail.

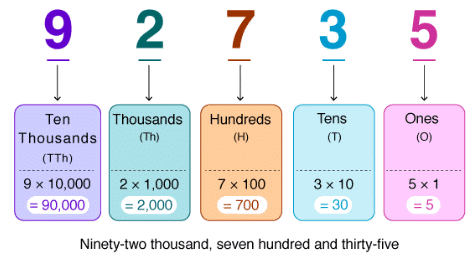
Now, let’s meet Creative Chitti, a calculator with buttons for +1, +10, +100, +1000, +10000, +100000, etc. I am Creative ChittiChitti shows that numbers can be made in many ways. For example, 5072 could be:

• (50 x 100) + (7 x 10) + (2 x 1) = 5000 + 70 + 2 = 5072
• (3 x 1000) + (20 x 100) + (72 x 1) = 3000 + 2000 + 72 = 5072
• Another way: (4 x 1000) + (10 x 100) + (6 x 10) + (12 x 1) = 4000 + 1000 + 60 + 12 = 5072

This leads us to the idea of expanded form. While Chitti is creative, Systematic Sippy wants to use the fewest button clicks possible. To make 5072 with the fewest clicks, Sippy would press:

• +1000 button: 5 times (for 5000)
• +100 button: 0 times (for 0 hundreds)
• +10 button: 7 times (for 70)
• +1 button: 2 times (for 2)

Total clicks = 5 + 0 + 7 + 2 = 14 clicks. The expression is: (5 x 1000) + (0 x 100) + (7 x 10) + (2 x 1) = 5072.

Notice something important? The way Systematic Sippy makes the number with the fewest clicks directly corresponds to the standard expanded form based on place value! Each digit is multiplied by its place value (ones, tens, hundreds, thousands, etc.).

Expanded Form: When we write a number in expanded form, we break it down to show the value of each digit. It’s like stretching the number out to see each part clearly.

Example 2: Write in expanded form: 4,582
Sol: Let’s expand 4,582:

1. Thousands place: The digit 4 is in the thousands place, so its value is 4,000.
2. Hundreds place: The digit 5 is in the hundreds place, so its value is 500.
3. Tens place: The digit 8 is in the tens place, so its value is 80.
4. Ones place: The digit 2 is in the ones place, so its value is 2.

Putting it all together:
4,582 = 4,000 + 500 + 80 + 2

Of Crores and Crores!

We’ve talked about lakhs, but the world of large numbers doesn’t stop there! What happens when we have numbers even bigger than ten lakhs?

As numbers get bigger, it becomes difficult to read and understand them unless they are written properly with commas. To help us, two main systems are used around the world:

• The Indian Number System
• The International Number System (also called the American System)

In the Indian system, the next major milestone after lakh is the crore as we already discussed above.

• 1 Crore = 100 Lakhs
• 1 Crore = 1,00,00,000 (That’s a 1 followed by seven zeros!)

Think back to the Creative Chitti calculator. If you pressed the +10,00,000 (ten lakh) button ten times, you would reach 1,00,00,000, which is one crore.

Just like lakhs, crores help us talk about very large quantities, such as the population of large cities or entire states, or the cost of major projects.

And it doesn’t stop at crores! The next step in the traditional Indian system is the arab.

• 1 Arab = 100 Crores
• 1 Arab = 1,00,00,00,000 (A 1 followed by nine zeros!)

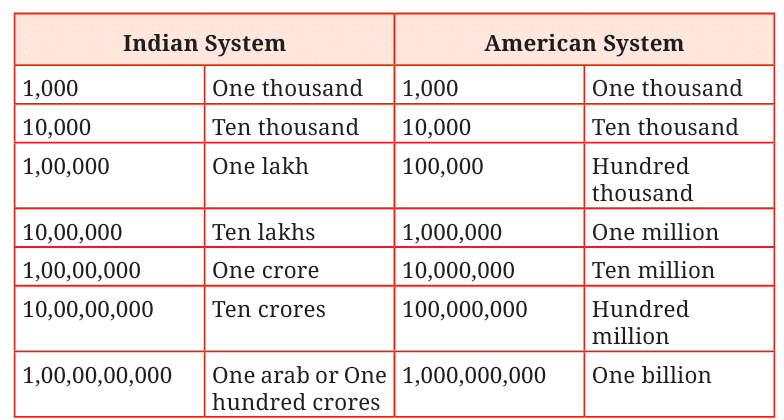
International System of Writing Numbers

• The number 100000 is read as one hundred thousand or 1 lakh. It is a 6-digit numeral. 
• In the International System, the number 10 lakh or ten hundred thousand, that is, a thousand thousand, is called a million. 
• It is written as under:

Instead of lakhs, crores, etc. as periods, we use millions, billions, etc.

• Let us write the smallest 8-digit number in the two systems of numerations.

• The International place value chart is given below.

• The chart can be expanded to include more than nine places.
• The section just before the millions is known as the billions section.
• Next, we have the trillions section.
• The places before the hundred billions are referred to as:
  – trillions place
  – ten trillions place
  – hundred trillions place
• When we compare the two systems of counting, we can see the following connections.

•  Note that in the Indian system, starting from the right after the first period of 3 digits all other periods are of 2 digits but in the International system, each period consists of three digits. 
•  We place a comma or leave space after every 3 digits. 
•  The abacus shows the number six million eight hundred forty-nine thousand two hundred forty. 
•  To make the task of reading and writing such large numbers easy, start counting digits from the right by threes and leave some space or put a comma after every three digits as shown below. 

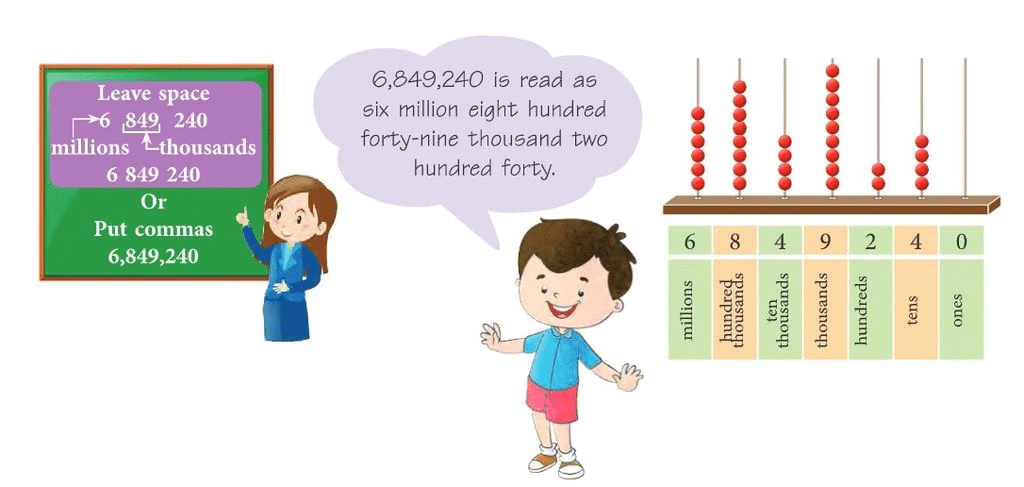
Try yourself:

What are the two main systems used to write large numbers around the world?

• A.Metric and Imperial
• B.Indian and International
• C.American and European
• D.Local and Global

View Solution

Number Names – Indian vs. American

Let’s take an example number:

→ 9876501234

• In the Indian system, we place commas like this:

9,87,65,01,234
We read it as:
9 arab 87 crore 65 lakh 1 thousand 234
or
987 crore 65 lakh 1 thousand 234

• In the American system, commas look like this:

9,876,501,234
We read it as:
9 billion 876 million 501 thousand 234

Understanding Zeros in Large Numbers

• 1 thousand = 1,000 → 3 zeros
• 1 lakh = 1,00,000 → 5 zeros
• 1 crore = 1,00,00,000 → 7 zeros
• 1 arab = 1,00,00,00,000 → 9 zeros

Now let’s answer these questions:

Q: How many zeros in a thousand lakh?

• 1 lakh = 1,00,000
• 1,000 × 1,00,000 = 1,00,00,00,000 → 8 zeros

But let’s calculate more carefully:

1000×1,00,000=1,00,00,00,000(which is actually 10 crores)

So the number has 8 zeros.

Q: How many zeros in a hundred thousand?

• 1 thousand = 1,000
• 100 × 1,000 = 1,00,000 → 5 zeros

So Ans: 5 zeros

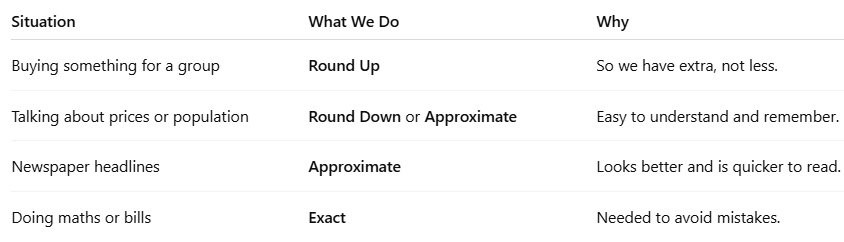
Exact and Approximate Values

Read the image above. Does this mean exactly 100,000 people walked through the gates? 
Probably not! It’s likely an approximation or an estimate. The actual number might have been 98,543 or maybe 101,210.
 For a headline, saying “about 1 lakh” gives a good enough idea of the crowd size without needing the precise count.

This brings us to the important concept of estimation. Often, especially with large numbers, we don’t need the exact value. An approximate value is easier to understand, remember, and use.

Why do we use approximate numbers?

Example:

• The exact population of Chintamani town is 76,068.
• But saying “about 75,000 people live there” gives a quick idea without needing to know the exact count.

Two Common Ways of Rounding:

1. Rounding Up:

• When we increase the number to a higher, easier number.
• Example: A school has 732 people. The principal may round it up and order 750 sweets.

2. Rounding Down:

• When we reduce the number a little to make it simpler.
• Example: An item costs ₹470, but the shopkeeper might say it’s around ₹450.

Let’s Summarise:

Nearest Neighbours

A common way to estimate is by rounding to the nearest ten, hundred, thousand, lakh, crore, etc. This involves looking at the digit to the right of the place value you’re rounding to.

Rule: If the digit to the right is 5 or greater, round up the digit in the target place value. If the digit to the right is 4 or less, keep the digit in the target place value the same. All digits to the right of the target place value become zeros.

Let’s find the nearest neighbours for 6,72,85,183:

• Nearest Thousand: 
  Look at the hundreds digit (1). 
  Since 1 < 5, keep the thousands digit (5) the same. 
   6,72,85,000
• Nearest Ten Thousand: 
  Look at the thousands digit (5). 
  Since 5 ≥ 5, round up the ten thousands digit (8) to 9. 
   6,72,90,000
• Nearest Lakh:
   Look at the ten thousands digit (8). 
  Since 8 ≥ 5, round up the lakhs digit (2) to 3. 
  6,73,00,000
• Nearest Ten Lakh: 
  Look at the lakhs digit (2). 
  Since 2 < 5, keep the ten lakhs digit (7) the same. 
   6,70,00,000
• Nearest Crore: 
  Look at the ten lakhs digit (7). 
  Since 7 ≥ 5, round up the crores digit (6) to 7. 
  7,00,00,000

Patterns in Products

Instead of multiplying directly by numbers like 5, 25, or 50, Roxie and Estu uses a shortcut based on how those numbers relate to 10, 100, or 1000.

These shortcuts are possible because:

• 5 = 10 ÷ 2
• 25 = 100 ÷ 4
• 50 = 100 ÷ 2
• 125 = 1000 ÷ 8

So, multiplying a number by 5 is the same as:

Dividing the number by 2 and then multiplying by 10
→ a × 5 = (a ÷ 2) × 10

And multiplying a number by 25 is the same as:

Dividing the number by 4 and then multiplying by 100
→ a × 25 = (a ÷ 4) × 100

These are based on properties of multiplication and division:

• Multiplication is associative and distributive
• You can rearrange factors in multiplication for easier calculation

For example:
a × 5 = a × (10 ÷ 2) = (a ÷ 2) × 10
This works because multiplication and division are inverse operations that can be grouped like this for easier solving.

Example 1: 116 × 5

Instead of directly multiplying 116 × 5, Roxie breaks it into:

116 × 5 = (116 ÷ 2) × 10

Why does this work?

• Because 5 = 10 ÷ 2, so multiplying by 5 is the same as dividing the number by 2 and then multiplying the result by 10.

So,

• 116 ÷ 2 = 58

Then, 58 × 10 = 580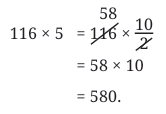Example 2: 824 × 25

Estu applies a similar shortcut:
824 × 25 = (824 ÷ 4) × 100
Why?

• Because 25 = 100 ÷ 4, so multiplying by 25 is like dividing by 4 and then multiplying the result by 100.
• So,
  • 824 ÷ 4 = 206
  • Then, 206 × 100 = 20600

Fascinating Facts about Large Numbers

This lesson uses real-world facts involving huge numbers to show how multiplication and divisionhelp us understand large quantities — like distances, weights, populations, and more.

1. Using Multiplication to Discover Big Facts

2. Using Division to Break Down Big Facts

Try yourself:

How many zeros are in a crore?

• A.5 zeros
• B.7 zeros
• C.9 zeros
• D.8 zeros

View Solution

Did You Ever Wonder….?

Estu’s Question:

Can the entire population of Mumbai fit into 1 lakh buses?

Step 1: Understand the Numbers

• 1 lakh buses = 1,00,000 buses
• Each bus holds = 50 people
• So, total people in 1 lakh buses =
  1,00,000 × 50 = 50,00,000 = 50 lakh people

Step 2: Compare with Mumbai’s Population

• Population of Mumbai = 1 crore 24 lakh = 1,24,00,000 people
• People buses can carry = 50 lakh

So, can everyone fit into the buses?
No! Because 1 crore 24 lakh is more than double 50 lakh.

Conclusion: The whole population of Mumbai cannot fit in 1 lakh buses.

Now think about the Titanic Ship:

Can the population of Mumbai fit into 5000 Titanic-like ships?

Step 1: How many people fit in 1 ship?

• Each Titanic can carry = 2,500 people
• So, 5000 ships can carry =
  5000 × 2500 = 1,25,00,000 = 1 crore 25 lakh people

Step 2: Compare again

• Mumbai’s population = 1 crore 24 lakh
• Space on ships = 1 crore 25 lakh

Yes! The population of Mumbai can fit into 5000 Titanic-like ships.

Solved Examples

Example 1: Write the number 70,53,138 in words using the Indian system.
Ans: Seventy lakh fifty-three thousand one hundred thirty-eight.

Example 2:  Write the number name “Fifty lakh five thousand fifty” in figures using the Indian system.
Ans: 50,05,050

Example 3: Compare 500 lakhs and 5 million. Use ‘<‘, ‘>’, or ‘=’.

Ans: 500 lakhs = 500 x 1,00,000 = 5,00,00,000

5 million = 5 x 1,000,000 = 5,000,000

Since 5,00,00,000 is much larger than 5,000,000,

500 lakhs > 5 million

Example 4: Using Systematic Sippy’s method (fewest clicks), how would you make the number 3,67,813? Write the expression.

Ans: +1,00,000 button: 3 times (3 lakhs)

+10,000 button: 6 times (6 ten thousands)

+1,000 button: 7 times (7 thousands)

+100 button: 8 times (8 hundreds)

+10 button: 1 time (1 ten)

+1 button: 3 times (3 ones) Total clicks = 3 + 6 + 7 + 8 + 1 + 3 = 28 clicks.

 Expression: (3 x 1,00,000) + (6 x 10,000) + (7 x 1,000) + (8 x 100) + (1 x 10) + (3 x 1)

Example 5: Round the number 3,87,69,957 to the nearest ten thousand.

Ans: Look at the digit in the thousands place: 9.

Since 9 ≥ 5, we round up the digit in the ten thousands place (6) to 7.

Rounded number: 3,87,70,000