Chapter Notes: Arithmetic Expressions

Introduction

Have you ever noticed how we combine numbers and operations like addition (+), subtraction (-), multiplication (×), and division (÷) to represent situations or solve problems? 
Phrases like “13 + 2” (13 plus 2), “20 – 4” (20 minus 4), or “12 × 5” (12 times 5) are common in mathematics. These combinations are called arithmetic expressions.

In this chapter, we will delve deeper into the world of arithmetic expressions. 

 Simple Expressions

• Every arithmetic expression has a specific value, which is the single number it represents. For instance, the expression “13 + 2” has a value of 15. 
• We use the equals sign (=) to show this relationship: 13 + 2 = 15. 
• Think about Mallika spending ₹25 each weekday (Monday to Friday) for lunch. To find her total weekly spending, we can write the expression 5 × 25. This expression represents “5 times 25,” and its value tells us the total amount spent.

An important point is that different expressions can result in the same value. Consider the number 12. It can be represented by various expressions:

• 10 + 2 = 12
• 15 – 3 = 12
• 3 × 4 = 12
• 24 ÷ 2 = 12

This flexibility allows us to express the same mathematical idea in multiple ways, which can be useful in different contexts or for simplifying problems. 

Comparing Expressions

Just as we compare individual numbers using symbols like equals (=), greater than (>), and less than (<), we can also compare arithmetic expressions. This comparison is based on the values that the expressions evaluate to.

For example, let’s compare the expressions 10 + 2 and 7 + 1:

• The value of 10 + 2 is 12.
• The value of 7 + 1 is 8.
• Since 12 is greater than 8, we can write: 10 + 2 > 7 + 1.

Similarly, let’s compare 13 – 2 and 4 × 3:

• The value of 13 – 2 is 11.
• The value of 4 × 3 is 12.
• Since 11 is less than 12, we write: 13 – 2 < 4 × 3.

 Reading and Evaluating Complex Expressions

Simple expressions usually involve just one operation. But what happens when an expression combines multiple operations, like 30 + 5 × 4? 
Without a clear context or rule, how do we know whether to add first or multiply first? This ambiguity can lead to different answers.

Consider the language example from the textbook:

• Sentence (a): “Shalini sat next to a friend with toys”. (Meaning: The friend has toys, Shalini sat next to her).
• Sentence (b): “Shalini sat next to a friend, with toys”. (Meaning: Shalini has the toys, and she sat next to her friend).

The comma in sentence (b) acts like punctuation, clarifying the meaning. Without it, the sentence could be interpreted in two ways. 
Similarly, in mathematics, we need rules and tools to ensure everyone evaluates a complex expression the same way.

Let’s look at this example: Mallesh brought 30 marbles, and Arun brought 5 bags with 4 marbles each. The total number of marbles can be written as 30 + 5 × 4.

• Purna’s calculation: Added 30 and 5 first (30 + 5 = 35), then multiplied by 4 (35 × 4 = 140).
• Mallesh’s calculation: Multiplied 5 and 4 first (5 × 4 = 20), then added 30 (30 + 20 = 50).

⇒ In the context of the story, Mallesh’s calculation (50 marbles) makes sense. Purna’s calculation (140 marbles) doesn’t fit the situation.
⇒ This highlights that just looking at the expression 30 + 5 × 4 isn’t enough; we need a standard order of operations.

⇒ To resolve such confusion and ensure consistent evaluation, mathematics uses specific tools and conventions, primarily brackets and the concept of terms, which we will explore next.

Try yourself:

What is the value of the expression 13 + 2?

• A.10
• B.20
• C.15
• D.12

View Solution

Brackets in Expressions

• One of the primary tools used in mathematics to clarify the order of operations in complex expressions is brackets ( ).
• When an expression contains brackets, the part of the expression inside the brackets must be evaluated first, before performing operations outside the brackets.

Let’s revisit the expression for the total number of marbles Mallesh and Arun brought: 30 + 5 × 4. 
We determined that multiplication should happen before addition based on the context. We can make this explicit using brackets:

30 + (5 × 4)

To evaluate this:

1. First, calculate the value inside the brackets: 5 × 4 = 20.
2. Then, perform the remaining operation: 30 + 20 = 50.

This use of brackets removes ambiguity and ensures the expression correctly represents the intended calculation.

Example 1: Irfan buys biscuits for ₹15 and toor dal for ₹56. He pays with ₹100. How much change does he get?

Ans: Irfan spent ₹15 on a biscuit packet and ₹56 on toor dal. 

So, the total cost in rupees is 15 + 56.

 He gave ₹100 to the shopkeeper. So, he should get back 100 minus the total cost.

 Can we write that expression as— 100 – 15 + 56 ? 

Can we first subtract 15 from 100 and then add 56 to the result?

 We will get 141. 

It is absurd that he gets more money than he paid the shopkeeper!

 We can use brackets in this case:

 100 – (15 + 56). 

Evaluating the expression within the brackets first, we get 100 minus 71, which is 29. 

So, Irfan will get back ₹29.

Example 2: Rani went to a stationery shop. She bought a notebook for ₹40 and a pen for ₹25. She gave the shopkeeper ₹100. How much money will she get back?

Step 1: Total cost of the items
₹40 + ₹25 = ₹65

Step 2: Amount given to the shopkeeper
₹100

Step 3: Expression to find the balance
100 – (40 + 25)

Step 4: Solve using brackets
= 100 – 65
= ₹35

Ans: Rani will get back ₹35.

Terms in Expressions

What if an expression has multiple operations but no brackets to specify the order, like 30 + 5 × 4? While brackets are one way to clarify order, another fundamental concept used is that of terms.

Terms are the parts of an expression separated by addition (+) signs.

To identify terms correctly, we first need to handle subtraction. Remember that subtracting a number is the same as adding its inverse (the number with the opposite sign). So, before identifying terms, we convert all subtractions into additions of negative numbers.

Let’s see some examples:

1. Expression:12 + 7
   • Already in addition form.
   • Terms: 12 and 7.
   • Marked: 12 + 7
2. Expression:83 – 14
   • Convert subtraction: 83 + (–14)
   • Terms: 83 and –14.
   • Marked: 83 + (–14)
3. Expression:–18 – 3
   • Convert subtraction: –18 + (–3)
   • Terms: –18 and –3.
   • Marked: –18 + (–3)
4. Expression:6 × 5 + 3
   • Already in addition form.
   • Notice that 6 × 5 does not contain an addition sign separating the 6 and 5. It represents a single value obtained through multiplication.
   • Terms: 6 × 5 and 3.
   • Marked: (6 × 5) + 3
5. Expression:2 – 10 + 4 × 6
   • Convert subtraction: 2 + (–10) + 4 × 6
   • Terms: 2, –10, and 4 × 6.
   • Marked: 2 + (–10) + (4 × 6)

Identifying terms is crucial for the standard order of operations:

1. Evaluate each term first: Perform all multiplications and divisions within each term.

2. Add the resulting values of the terms: Once each term has been simplified to a single number, perform the additions (including the additions that came from converted subtractions).

Let’s re-evaluate 30 + 5 × 4 using terms:

1. Identify terms: 30 and 5 × 4.
2. Evaluate each term: The term 30 is already evaluated. The term 5 × 4 evaluates to 20.
3. Add the term values: 30 + 20 = 50.

This process of identifying and evaluating terms provides a systematic way to handle expressions with multiple operations, even without brackets, ensuring a consistent result.

Swapping and Grouping 

Once we have identified the terms in an expression (after converting all subtractions to additions), does the order in which we add these terms matter?
 Let’s investigate.

Consider the expression 6 – 4. Converting to addition gives 6 + (–4).

• The terms are 6 and –4.
• The value is 6 + (–4) = 2.

What if we swap the terms? –4 + 6.

• The value is –4 + 6 = 2.

The value remains the same! This isn’t just true for positive numbers; it holds even when negative numbers are involved. 
Swapping any two terms in an addition expression does not change the final value.

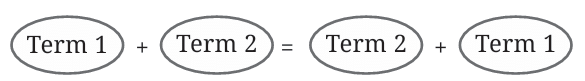
This property is formally known as the Commutative Property of Addition.

Now, consider an expression with three terms, like (–7) + 10 + (–11).

Let’s try adding them in different groups:

1. Group the first two terms:( (–7) + 10 ) + (–11)= ( 3 ) + (–11)= –8
2. Group the last two terms:(–7) + ( 10 + (–11) )= (–7) + ( –1 )= –8

Again, the value is the same regardless of how we group the terms for addition. This also holds true for expressions with more than three terms and when negative numbers are involved.

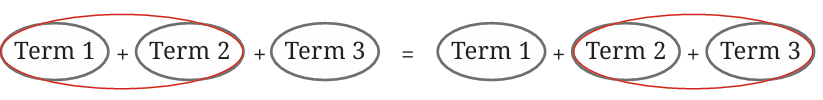
This property is formally known as the Associative Property of Addition.

Try yourself:

What is the name of the property that states the grouping of terms does not affect the sum?

• A.Identity Property of Addition
• B.Distributive Property
• C.Commutative Property of Addition
• D.Associative Property of Addition

View Solution

Conclusion: Order Doesn’t Matter for Addition

Because of the commutative and associative properties, when an expression only involves addition (after converting subtractions), we can add the terms in any order or grouping we find convenient, and the result will always be the same.

For example, in (–7) + 10 + (–11), we could add the negative terms first: (–7) + (–11) = –18, and then add the positive term: –18 + 10 = –8.

In mathematics we use the phrase commutative property of addition instead of saying “swapping terms does not change the sum”. Similarly, “grouping does not change the sum” is called the associative property of addition.

Swapping the Order of Things in Everyday Life 

Manasa’s mom says:
“Wear your hat and shoes.”

Manasa can do either:

• Wear her hat first, then her shoes, or
• Wear her shoes first, then her hat.

Result:
Manasa will still be ready to go out and look the same either way.
➡ Here, the order does not matter.

In math, this is like:
2 + 3 = 5 and 3 + 2 = 5
Addition can be done in any order — it won’t change the answer

Order 

Does

 Matter

Now her mom says:
“Wear your socks and shoes.”

This time:

• If Manasa wears socks first, then shoes — ✅ that’s the correct way.
• But if she wears shoes first, then tries to wear socks — ❌ it’s wrong and uncomfortable!

Result:
She’ll look odd and it won’t work properly.
➡ Here, the order matters.

In math, this is like:
8 – 5 = 3, but 5 – 8 = -3
So in subtraction, changing the order changes the answer.

More Expressions and Their Terms

Let’s look at a few more examples from the textbook to solidify our understanding of writing expressions and identifying their terms in different scenarios.

Example: Amu, Charan, Madhu, and John went to a hotel and ordered four dosas. Each dosa cost ₹23, and they wish to thank the waiter by tipping ₹5. Write an expression describing the total cost.

• Situation: 4 friends order 4 dosas at ₹23 each and want to leave a ₹5 tip.
• Expression for total cost: The cost of the dosas is 4 × 23. The tip is 5. The total cost is the sum: 4 × 23 + 5.
• Identifying Terms: The expression is already a sum. The terms are 4 × 23 and 5.
• Evaluation:
  1. Evaluate terms: 4 × 23 = 92. The term 5 is already evaluated.
  2. Add term values: 92 + 5 = 97.
• Total Cost: ₹97.

Example : Children in a class are playing “Fire in the mountain, run, run, run!”. Whenever the teacher calls out a number, students are supposed to arrange themselves in groups of that number. Whoever is not part of the announced group size, is out. Ruby wanted to rest and sat on one side. The other 33 students were playing the game in the class. The teacher called out ‘5’. 

• Situation: 33 students are playing. The teacher calls out ‘5’. Students form groups of 5. Ruby observes.
• Observation: Ruby sees 6 full groups of 5, with 3 students left over.
• Expression: Ruby writes 6 × 5 + 3 (representing 6 groups of 5, plus the 3 remaining).
• Identifying Terms: The terms are 6 × 5 and 3.
• Evaluation:(6 × 5) + 3 = 30 + 3 = 33 (the total number of students playing).
• Variations:
  • If the teacher called ‘4’: There would be 8 groups of 4 with 1 left over. Expression: 8 × 4 + 1. Terms: 8 × 4 and 1.
  • If the teacher called ‘7’: There would be 4 groups of 7 with 5 left over. Expression: 4 × 7 + 5. Terms: 4 × 7 and 5.

Example: Raghu bought 100 kg of rice from the wholesale market and packed them into 2 kg packets. He already had four 2 kg packets. Write an expression for the number of 2 kg packets of rice he has now and identify the terms.  

• Situation: Raghu buys 100 kg rice, packs it into 2 kg bags. He already had 4 such bags.
• Expression for total bags: Number of new bags = 100 ÷ 2 (or 100/2). Total bags = 4 + 100 ÷ 2.
• Identifying Terms: The terms are 4 and 100 ÷ 2.
• Evaluation:
  1. Evaluate terms: 4 is evaluated. 100 ÷ 2 = 50.
  2. Add term values: 4 + 50 = 54.
• Total Bags: 54 bags.

Example: Kannan has to pay ₹432 to a shopkeeper using coins of ₹1 and ₹5, and notes of ₹10, ₹20, ₹50 and ₹100. How can he do it?

• Situation: Paying ₹432 using various denominations.
• Possibility 1 Expression:4 × 100 + 1 × 20 + 1 × 10 + 2 × 1
  • Terms:4 × 100, 1 × 20, 1 × 10, 2 × 1.
  • Evaluation:400 + 20 + 10 + 2 = 432.
• Possibility 2 Expression:8 × 50 + 1 × 10 + 4 × 5 + 2 × 1
  • Terms:8 × 50, 1 × 10, 4 × 5, 2 × 1.
  • Evaluation:400 + 10 + 20 + 2 = 432.
• This shows how expressions can represent real-world combinations, and identifying terms helps understand the structure.

Example: Here are two pictures. Which of these two arrangements matches with the expression 5 × 2 + 3?

Which image is correct?

• Expression:5 × 2 + 3
• Identifying Terms:5 × 2 and 3.
• Evaluation: 
• Interpretation: The expression means “3 more than 5 groups of 2”. This matches the picture showing 5 pairs of items plus 3 individual items.This Image is correct

Removing Brackets — I

Let us find the value of this expression, 

200 – (40 + 3). 

We first evaluate the expression inside the bracket to 43 and then subtract it from 200. But it is simpler to first subtract 40 from 200:

 200 – 40 = 160.

 And then subtract 3 from 160: 

160 – 3 = 157. 

What we did here was 200 – 40 – 3. Notice, that we did not do

 200 – 40 + 3. 

So, 

200 – (40 + 3) = 200 – 40 – 3.

Removing Brackets – II

Example: Lhamo and Norbu went to a hotel. Each of them ordered a vegetable cutlet and a rasgulla. A vegetable cutlet costs ₹43 and a rasgulla costs ₹24. Write an expression for the amount they will have to pay.

Situation:
Lhamo and Norbu each buy:

• 1 vegetable cutlet = ₹43
• 1 rasgulla = ₹24

So, the amount one person pays is:
43 + 24

There are two people, so together they pay:
(43 + 24) + (43 + 24)
Instead of writing it this way, we can simplify using brackets and multiplication:
2 × (43 + 24)

Why use brackets?
Brackets tell us to first add the items, and then multiply the total by 2 (for two people).
So,
2 × (43 + 24) = 2 × 67 = ₹134

This is much simpler than adding 43 + 24 twice!

What if another friend, Sangmu  joins?

If a third person, Sangmu, joins and buys the same items, then the expression becomes:
3 × (43 + 24)
That means: 3 × 67 = ₹201

Example: In the Republic Day parade, there are boy scouts and girl guides marching together. The scouts march in 4 rows with 5 scouts in each row. The guides march in 3 rows with 5 guides in each row (see the figure below). How many scouts and guides are marching in this parade?

Boy scouts: 4 rows × 5 boys = 20
Girl guides: 3 rows × 5 girls = 15

So total people = 20 + 15 = 35

But we can do this smarter:
Instead of calculating separately, first add the rows:
(4 + 3) × 5 

Computing these expressions, we get

(4 + 3) × 5 = 7 × 5 = 35

What’s the lesson here?

Using brackets helps us to group numbers and make multiplication or subtraction easier.
For example:

Distributive Property:

• (a + b) × c = a × c + b × c
• (a – b) × c = a × c – b × c

Example:
(10 + 3) × 98 = 10 × 98 + 3 × 98 = 13 × 98

This makes solving faster and more organized.

The multiple of a sum (or difference) = sum (or difference) of the multiples.

Solved Examples

Example 1:  Evaluate 30 + 5 × 4

Expression:30 + 5 × 4Identify Terms: The terms are 30 and 5 × 4.
Evaluate Terms:

• 30 is already evaluated.
• 5 × 4 = 20.

Add Term Values:30 + 20 = 50.
Answer: 50

Example 2: Evaluate 100 – (15 + 56)

Expression:100 – (15 + 56)

Evaluate Inside Brackets First:15 + 56 = 71.

Perform Remaining Operation:100 – 71 = 29.

Answer: 29

Example 3: Evaluate 4 × 23 + 5

Expression:4 × 23 + 5

Identify Terms:4 × 23 and 5.

Evaluate Terms:

• 4 × 23 = 92.
• 5 is already evaluated.

Add Term Values:92 + 5 = 97.

Answer: 97